May 1, 2023 · buildx rust probabilistic datastructure

What is HyperLogLog and how to build yours in Rust

Typically, counting the number of unique values in a dataset is an easy problem. You maintain a BST or HashSet to remove duplicates as they come in while keeping track of the count of inserted unique values. It takes O(n) space, which is acceptable for smaller datasets.  However, for large datasets, storage becomes quickly expensive, especially if you would like to keep track of counts in real-time.

Let's say that you are working on a banking application that processes ~1 billion transactions every day. You would like to know the number of unique customer account numbers on which transactions were made but you have limited memory and computational resources. Let's do a back-of-the-envelope calculation for the memory required if we were to go the route of a HashSet.

a. Assume 10% of the transactions originate from unique account numbers = 10 million 
b. Assume Customer account numbers are 10 digit numbers. 
c. Each account number could be represented by a long datatype.

                                ---

10 million account numbers * 8 bytes = 80 MB in memory

💡
Note that the earlier calculation does not include the storage required for the hashes in the set or the pointer to the next link in the chain (due to collisions).

One other alternative is to persist all the account numbers to a file or a database and run a map-reduce/distinct operation at a regular frequency.  However, it requires a fair amount of work and also the output is not real-time.

This sounds like an impossible task but you'll see shortly how we could leverage an algorithm called HyperLogLog to get a "close to actual" estimate of unique values in a dataset by using an incredibly small fraction of storage.  For the case of account numbers that we discussed above, if you can live with a 1% error rate, you'll just need 1 MB with HLL.

What is HyperLogLog?

HyperLogLog is an algorithm that allows for a highly accurate "estimation" of the number of distinct elements in a dataset. More formally, HyperLogLog is a probabilistic algorithm used for estimating the cardinality in a set.

Several popular databases and frameworks use HLL underneath to provide quick estimates of distinct values - Apache Spark, Cassandra, MongoDB, Redis, Druid, etc.

How does it work?

Let us consider the case where the account number just has one digit. There are 10 possible account numbers: 0 to 9 and each account number has an equal probability of occurrence. Therefore, the probability of seeing the account number 0 in one of the transactions is 1/10.  Let's now consider the case where the account number has 2 digits. Account numbers can be between 00 and 99. Again, the possibility of us seeing 00 is 1/100. To generalize this, the possibility of seeing k number of leading zeros in an account number of any size is :

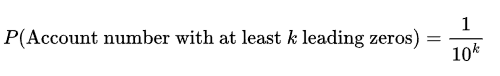
Applying this, we can "kinda" conclude that if we saw an account number with 2 leading zeros (00) in our transactions, we have seen 100 (k=2) account numbers. (Hang in there, for now.)

HyperLogLog follows exactly the same approach of looking at leading zeros, except that, in order to represent all kinds of data and not just numbers, it uses the binary representation of a hashed value of an element instead of using the actual data. (Some implementations use trailing zeros but as far as the hashes are uniformly distributed, it doesn't affect the accuracy.)

Since the data is binary, it is easy to see that the occurrence of 0 in a single-digit binary is 1/2, 00 in a two-digit binary is1/4 , and so on.  So, our estimation formula changes as:

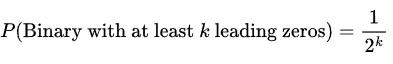
So, if we have seen an account number with 2-leading zero in its binary representation, we can "kinda" conclude that we have seen at least 4 unique account numbers.

Very incorrect estimates

You'll quickly realize that we could estimate only in exponents of 2, which results in overestimation or underestimation. Also, imagine the situation when your first account number has 7 leading zeros.  The HLL will immediately report that we have seen 127 unique accounts when we just saw 1.

Solution

In order to circumvent this problem Flajolet and Martin, the authors of the algorithm, proposed four major changes to their algorithm:

  1. Use multiple hash functions and average the estimates from each bucket of the hash function.
  2. Instead of using arithmetic mean to find the average, use harmonic mean.
  3. Use different bias corrections based on the total number of buckets used and
  4. Use correction for large and small estimates.

Through these changes, the error rate of the algorithm is brought down to

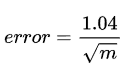
What this would also mean is that we could specify an error rate while instantiating an HLL and the buckets/registers (m) size would be adjusted to meet that error rate.  For all practical purposes, the error rate is significantly small.

Now, let's go over each of the improvements one by one:

1. Multiple buckets

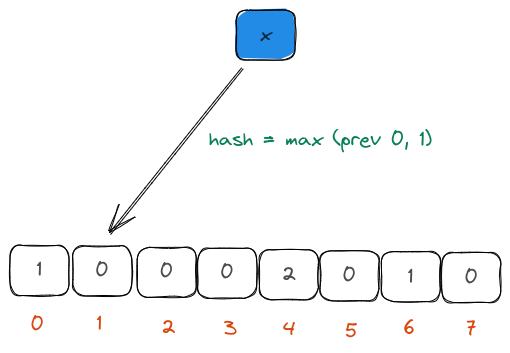
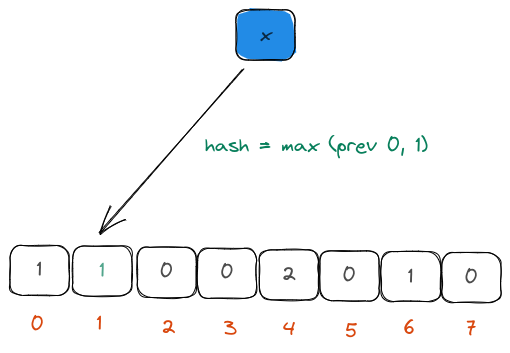
We could use a handful of hash functions to hash the input element. We could then compute the count of leading zeros in the hash binary. This count is then stored in the buckets that the hash belongs to (which could be derived through a simple modulus operator).

Unfortunately, computing multiple hashes is expensive for large datasets and therefore, the authors decided to use the first few bits of the binary representation of the hash to decide the bucket. This was very cheap to compute.

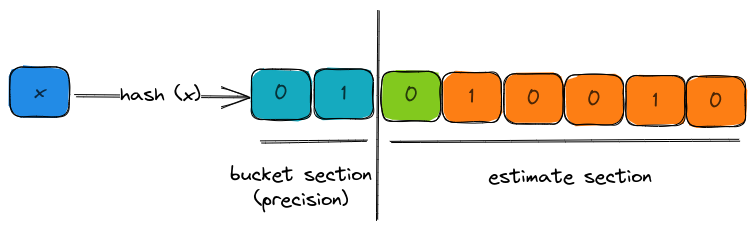
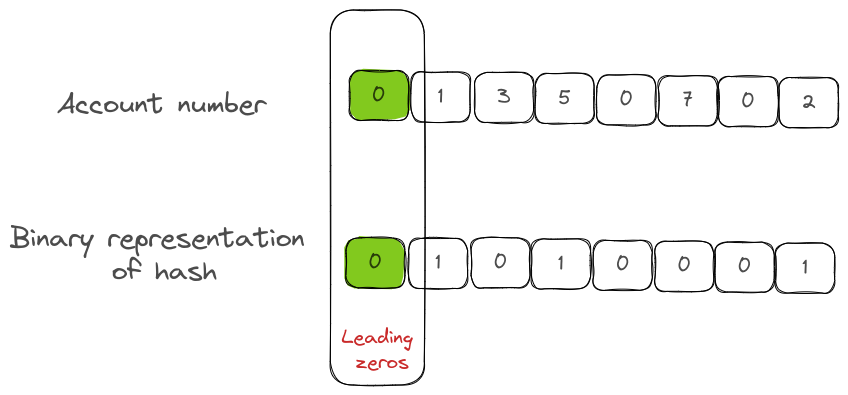
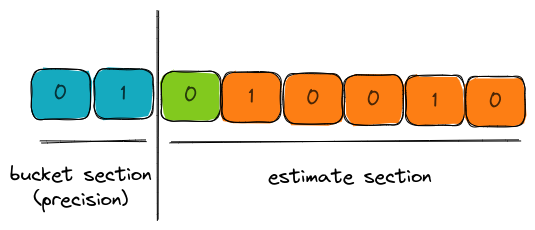
In the visual above, the 8-bit binary representation of the hash has two parts,

  1. bucket section (aka precision): the bits that decide which bucket does this hash output affect the estimates of.
  2. estimate section: the set of bits for computing the leading zeros.

In this case, the bucket is 1 and the estimate is 1 due to the presence of 1 leading zero.

2. Use harmonic mean

The Harmonic mean is the reciprocal of the average of the reciprocals of the numbers. It is given by:  

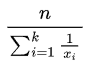
So, for our 8 buckets with estimations 1, 1, 2, 1 , we do:

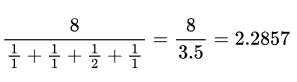
3. Use correction factor based on bucket size

Ours is a contrived example and therefore the number of buckets that we have is 8. Typically, the bucket sizes are minimally 16. The bias correction (alpha) mentioned in the paper are :

During our final estimation, we multiply the raw estimates (in our case 2.2857) by this alpha correction factor.

4. Use correction factor based on estimate size

As a final step, one round of correction is also done based on how large or small the estimate is, in comparison to the bucket size.

There are three ranges:

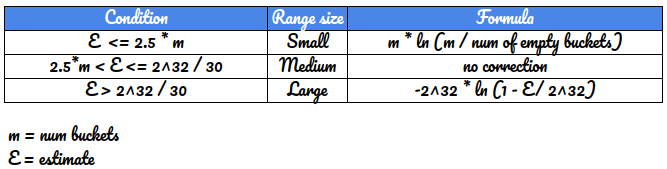
(I have absolutely no idea how these numbers are derived. These are just lifted from Page 14 of the original paper)

5. Final estimate

The formula to derive the final estimate from the raw estimate is:

final_estimate = range_size_correction(alpha * raw_estimate)

That's it! Now that we have all the theory out of the way, let's implement the algorithm in Rust.

Implementation in Rust

1. Instantiation

There's just one input parameter required for HLL, which is your expected error rate. As we saw before, the bucket size is adjusted based on the error rate.

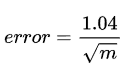
The number of buckets is calculated as:

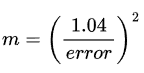
A recommended set of bits (bucket section/precision) used to identify the bucket is log2(m)

Putting them all together in our new function: 

pub struct HyperLogLog<T: Hash + Eq> {
    alpha: f64,
    precision: usize,
    num_buckets_m: usize,
    buckets: Vec<u8>,
    hasher: SipHasher24,
    _p: PhantomData<T>,
}

impl<T: Hash + Eq> HyperLogLog<T> {
    pub fn new(error_rate: f64) -> Result<Self> {
        validate(error_rate)?;
        let precision = (1.04 / error_rate).powi(2).log2().ceil() as usize; // log2(m)
        let num_buckets_m = 1 << precision; // 2^precision
        let alpha = calculate_alpha(num_buckets_m)?;

        //Instantiate our single hashing function
        let random_key = generate_random_seed();
        let hasher = create_hasher_with_key(random_key);

        let hll = HyperLogLog {
            alpha,
            precision,
            num_buckets_m,
            buckets: vec![0; num_buckets_m],
            hasher,
            _p: PhantomData,
        };

        Ok(hll)
    }

The alpha function just encodes the table that we saw previously: 

fn calculate_alpha(num_buckets_m: usize) -> Result<f64> {
    if num_buckets_m < 16 {
        return Err(InputError(format!(
            "Invalid number of buckets calculated {num_buckets_m}"
        )));
    }
    let alpha = match num_buckets_m {
        16 => 0.673,
        32 => 0.697,
        64 => 0.709,
        _ => 0.7213 / (1.0 + 1.079 / num_buckets_m as f64),
    };

    Ok(alpha)
}
//Hash helper functions

/// Generates a random 64-bit key used for hashing
pub fn generate_random_seed() -> [u8; 16] {
    let mut seed = [0u8; 32];
    getrandom::getrandom(&mut seed).unwrap();
    seed[0..16].try_into().unwrap()
}

/// Creates a `SipHasher24` hasher with a given 64-bit key
pub fn create_hasher_with_key(key: [u8; 16]) -> SipHasher24 {
    SipHasher24::new_with_key(&key)
}

2. Building the APIs

a. Insert

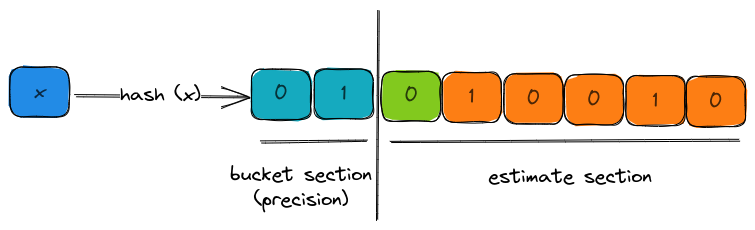
In the insertion function, as we saw earlier,

  1. The precision and the estimate bits as separated.
  2. The precision bits are used to identify the bucket that we are going to update the new estimate.
  3. The estimate bits are examined for the leading zeros.
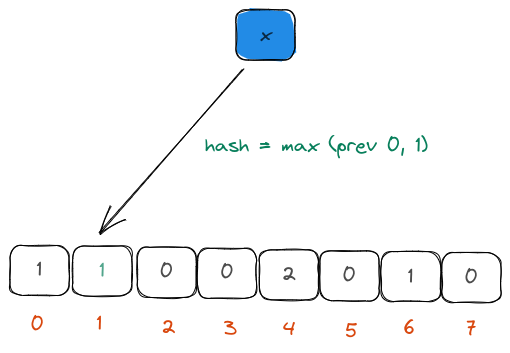
  4. The previous estimate in the bucket is examined and updated with the new estimate, if necessary.

Separate precision and estimation bits

Compare previous and current estimate and update bucket if necessary

pub fn insert<Q>(&mut self, item: &Q)
    where
        T: Borrow<Q>,
        Q: Hash + Eq + ?Sized,
    {
        let mut hasher = self.hasher;
        item.hash(&mut hasher);
        let hash = hasher.finish();

        let bucket_index = (hash >> (64 - self.precision)) as usize; // Take the first precision bits
        let estimate_bits_mask = (1 << (64 - self.precision)) - 1; // Create a mask for excluding the precision bits
        let estimate_bits = hash & estimate_bits_mask;
        let trailing_zeros = estimate_bits.leading_zeros() as u8 + 1; // Count the number of leading zeros
        let prev_estimate = self.buckets[bucket_index]; // Get the previous estimate
        self.buckets[bucket_index] = max(prev_estimate, trailing_zeros) // Update the estimate if necessary
    }

b. Estimate

For the estimate, we would

  1. calculate the raw estimate by using harmonic mean.
  2. multiply the estimate with the previously calculated alpha.
  3. arrive at final estimate after correcting for size of estimates in comparison to bucket size.

The correct_for_estimate_size function just encodes our previous table:

fn correct_for_estimate_size(&self, raw_estimate: f64, m: f64, empty_registers: usize) -> f64 {
        match raw_estimate {
            //Small range correction
            sr if raw_estimate <= 2.5_f64 * m => {
                if empty_registers > 0 {
                    m * (m / empty_registers as f64).ln()
                } else {
                    sr
                }
            }
            //Medium range correction
            mr if raw_estimate <= (TWO_POW_32 / 30.0_f64) => mr,
            //Large range correction
            lr => -TWO_POW_32 * (1.0 - lr / TWO_POW_32).ln(),
        }
    }

The estimate function calculates the harmonic mean and factors in alpha and estimate size correction. 

    pub fn estimate(&self) -> usize {
        let m = self.num_buckets_m as f64;

        let mut sum = 0.0_f64;
        let mut empty_registers = 0;
        for &v in self.buckets.iter() {
            sum += 2.0_f64.powf(-(v as f64));
            if v == 0 {
                empty_registers += 1;
            }
        }

        let raw_estimate = self.alpha * m.powi(2) / sum;
        let estimate = self.correct_for_estimate_size(raw_estimate, m, empty_registers);

        estimate as usize
    }

Code

The complete code is here.