Build your own Counting Bloom Filter in Rust

A Counting Bloom Filter is a probabilistic data structure that helps us quickly check if an element is present in a set or not. You might argue "Hey, can't a simple Set do it?".

Yes, indeed and to top it, Counting Bloom Filter is not even 100% accurate and expects us to provide the expected "false positive rate". Where Bloom Filters shine is that for large volumes of data it would use much lesser memory than a regular HashSet.

This post attempts an implementation of the datastructure. At the end of the post, you'll be able to build your own Counting Bloom Filter. The final code is available here.

Before we get into the implementation, let's get some properties of CBF out of the way:

1. As with our traditional BloomFilter, Quotient Filter or CuckooFilter, Counting Bloom Filter is a probabilistic data structure that is used to test whether an element is a member of a set. Essentially, these filters aim to solve a class of problems called "Membership".  A key feature that CBF offers over traditional Bloom Filter is that CBF allows deletion of inserted items.
2. As with any probabilistic data structure, there is a chance that we might get some false positives - essentially, the response to the question "Is an element present in the set?"   is not 100% accurate. There are times when the bloom filter would say that the element is present but it actually was not.  This "false positive" rate is configurable through a parameter.
3. Unlike HashSet, you cannot iterate through the values stored in the set - we can only check whether the value is present in the CBF.

Bloom Filter vs Counting Bloom Filter

The underlying storage of a BloomFilter is just a fixed-size array of bits.

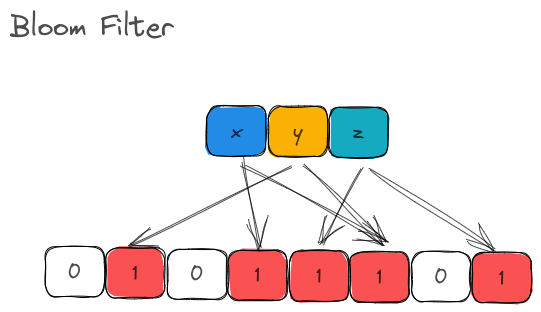
A Counting Bloom Filter uses a fixed-size array of counters.

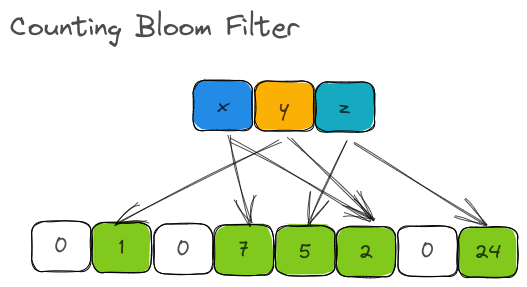
To put it in crude terms, the underlying storage of Bloom Filter is a Vec<bool> (or a BitSet). With CBF, it is a Vec<u8> or Vec<u16> or Vec<u32> or a list of unsigned integers.

For illustration, our implementation of a Counting Bloom Filter will use a u8 bit counter.  

Setting the stage

1. Declaring our struct and instantiation

#[derive(Debug)]
pub struct CountingBloomFilter<T: ?Sized + Hash> {
    counter: Vec<u8>,
    m: usize,
    k: usize,
    hasher: SipHasher24,
    expected_num_items: usize,
    false_positive_rate: f64,
    len: usize,
    _p: PhantomData<T>,
}

As expected, our struct encapsulates a list of counters.  There are two parameters that we would be accepting from the user, which are expected_num_items and false_positive_rate.

1. The expected_num_items is an approximate number of items that the user would like to store in the CBF.
2. The false_positive_rate is an estimate of False Positives/inverse accuracy that the user can live with.

The len just stores the total number of items inserted into the data structure so far. We'll discuss the m and k fields in the next section.  

2. Number of buckets and number of hashes

Bloom Filter

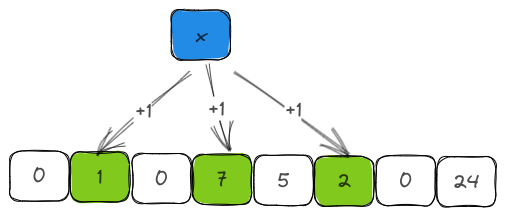
In a BloomFilter, m is simply the size of the bit vector (or underlying bits representing the membership of the various inserted values). k is the number of hash functions that each inserted value has to be run against.

So, given a value x, it will be hashed by k number of hash functions and the corresponding bit in the m buckets will be set to True.

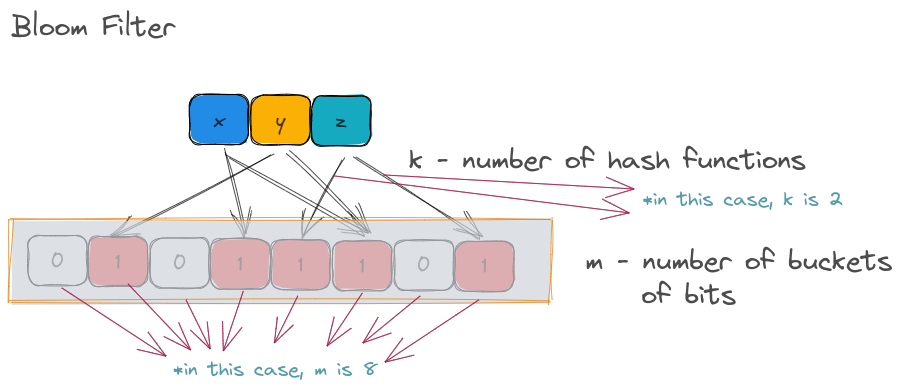
Let's consider the illustration above. Each item ( x, y, z) are hashed by 2 hash functions (represented by arrows). The resulting output are expected to be the bucket indices. Considering the total number of buckets is just 8 in the above illustration, the output of the hash function is modulo-ed to reduce the range between 0 and 7.

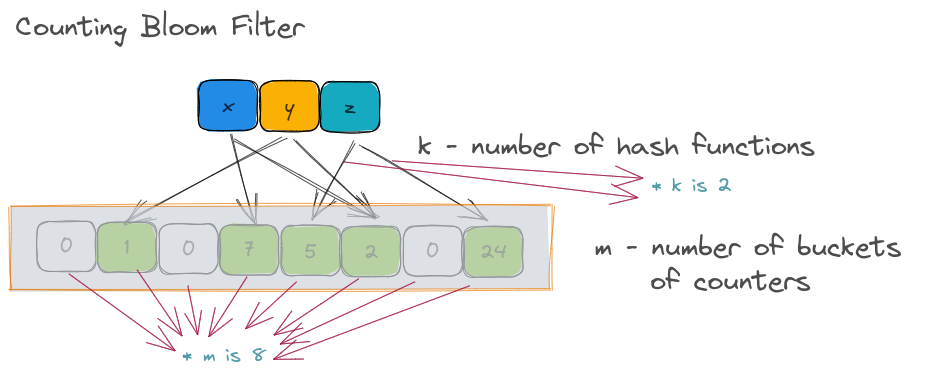
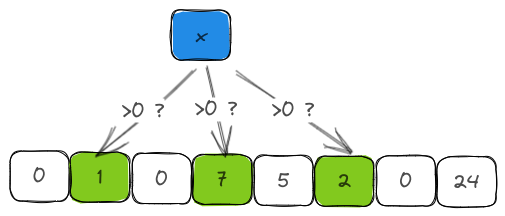
Counting bloom filter.

The number of hash functions ( k ) is 2 as above and the m is 8. However, the underlying store is not a list of bits but a list of counters.

The formulas for calculating the size of m and k given the expected_num_of_items and false_positive_rate for Counting Bloom Filter are:

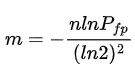
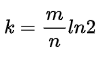
Let's implement the optimal_m, optimal_k and the new functions

fn optimal_m(num_items: usize, false_positive_rate: f64) -> usize {
    -(num_items as f64 * false_positive_rate.ln() / (2.0f64.ln().powi(2))).ceil() as usize
}

fn optimal_k(n: usize, m: usize) -> usize {
    let k = (m as f64 / n as f64 * 2.0f64.ln()).round() as usize;
    if k < 1 {
        1
    } else {
        k
    }
}

impl<T: ?Sized + Hash + Debug> CountingBloomFilter<T> {
    pub fn new(expected_num_items: usize, false_positive_rate: f64) -> Result<Self> {
        validate(expected_num_items, false_positive_rate)?;
        let m = optimal_m(expected_num_items, false_positive_rate);
        let counter = vec![0; m];
        let k = optimal_k(expected_num_items, m);
        let random_key = generate_random_key();
        let hasher = create_hasher_with_key(random_key);
        Ok(Self {
            counter,
            m,
            k,
            hasher,
            expected_num_items,
            false_positive_rate,
            len: 0,
            _p: PhantomData,
        })
    }

As you can see, only the "estimated number of items to be inserted" and the "false positive rate" is needed to construct our Counting Bloom Filter.

3. Hashers

Once we calculate the optimal number of hash functions (k), we need to create k independent hash functions. One approach is to have a repository of hash functions and initiate them with a random key. However, there is a simpler approach that is proposed by Adam Kirsch and Michael Mitzenmacher, where we could simulate additional hash functions with the help of two base hash functions.  

Quoting the paper:

The idea is the following: two hash functions h1(x) and h2(x) can simulate more than two hash functions of the form gi(x) = h1(x) + ih2(x). In our context i will range from 0 up to some number k − 1 to give k hash functions, and the hash values are taken modulo the size of the relevant hash table.

Specifically, only two hash functions are necessary to effectively implement a Bloom filter without any increase in the asymptotic false positive probability. This leads to less computation and potentially less need for randomness in practice.

Essentially, we just need 2 independent hash functions to simulate k hash functions. Typically, Bloom Filters use 64-bit hash functions since they create enough bits for us to populate the buckets uniformly.  In our implementation, we will use a 128-bit hash function and use the first and the second 64 bits to simulate two hash function outputs. We will then use these two 64-bit hashes to create more hashes.

Firstly, in order to provide a random seed to our 128-bit hasher, we'll use the generate_random_key function.

use siphasher::sip128::SipHasher24;

/// Generates a random 128-bit key used for hashing
fn generate_random_key() -> [u8; 16] {
    let mut seed = [0u8; 32];
    getrandom::getrandom(&mut seed).unwrap();
    seed[0..16].try_into().unwrap()
}

/// Creates a `SipHasher24` hasher with a given 128-bit key
fn create_hasher_with_key(key: [u8; 16]) -> SipHasher24 {
    SipHasher24::new_with_key(&key)
}

Building the APIs

With all the foundational functions out of the way, let us get into implementing the API - the three functions insert, contains and delete

1. Insert

When an element is inserted into the filter, the counters corresponding to the element's hash values are incremented by one. This is in contrast to BloomFilter where we just set the corresponding bit. While we do this, we will also use this opportunity to keep track of the number of items inserted into the bloom filter by incrementing the len field.

  pub fn insert(&mut self, item: &T) {
        self.get_set_bits(item, self.k, self.m, self.hasher)
            .iter()
            .for_each(|&i| self.counter[i] = self.counter[i].saturating_add(1));
        self.len += 1;
  }

The get_set_bits is a helper function that takes the item to be inserted and returns the indices of all buckets for whom the counters need to be incremented. Essentially, the get_set_bits function

1. Takes an item as an input
2. Creates a 128-bit hash (done in get_hash_pair)
3. Splits the 128-bit hash into 2 parts, thereby creating the 2 base hashes (done in get_hash_pair)
4. Creates k hashes out of the 2 base hashes using the Kirsch and Mitzenmacher method
5. Since we just have m buckets and the hash function output could be bigger, we do a modulus of m on each hash output. This returns k bucket indices on m . These are the indices of the counters in the bucket that needs to be incremented.

    fn get_set_bits(&self, item: &T, k: usize, m: usize, hasher: SipHasher24) -> Vec<usize> {
        let (hash1, hash2) = self.get_hash_pair(item, hasher);
        let mut set_bits = Vec::with_capacity(k);
        if k == 1 {
            let bit = hash1 % m as u64;
            set_bits.push(bit as usize);
            return set_bits;
        }
        for ki in 0..k as u64 {
            let hash = hash1.wrapping_add(ki.wrapping_mul(hash2));
            let bit = hash % m as u64;
            set_bits.push(bit as usize);
        }
        assert!(set_bits.len() == k);
        set_bits
    }
    
     /// Computes the pair of 64-bit hashes for an item using the internal hasher
    fn get_hash_pair(&self, item: &T, mut hasher: SipHasher24) -> (u64, u64) {
        item.hash(&mut hasher);
        let hash128 = hasher.finish128().as_u128();
        let hash1 = (hash128 & 0xffff_ffff_ffff_ffff) as u64;
        let hash2 = (hash128 >> 64) as u64;
        (hash1, hash2)
    }

2. Contains

As you might have guessed already, testing whether an item is present in the filter is just a matter of computing the hashes for the item and checking whether the counters in the bucket corresponding to the hashes have a non-zero value.

    pub fn contains(&self, item: &T) -> bool {
        self.get_set_bits(item, self.k, self.m, self.hasher)
            .iter()
            .all(|&i| self.counter[i] > 0)
    }

3. Delete

The deletion operation is just an inverse of the insertion operation with two additional nuances.

1. We can only delete an item that is already present in the filter. So, we check for it by calling the contains.
2. Our counter can never be less than 0. So, we use the saturating_sub function to ensure that.

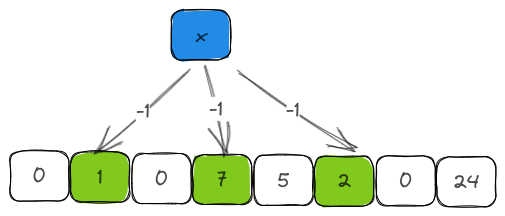
	pub fn delete(&mut self, item: &T) {
        let is_present = self.contains(item);
        if is_present {
            self.get_set_bits(item, self.k, self.m, self.hasher)
                .iter()
                .for_each(|&i| {
                    self.counter[i] = self.counter[i].saturating_sub(1);
                });
            self.len -= 1;
        }
    }

4. Estimated count

Although Counting Bloom Filter is not the best data structure to get an estimated count of an item, it is not uncommon to see instances where the function is implemented. Estimated count is arrived at by looking at all the counter values and picking the minimum of those values.  The reasoning behind choosing minimum and not maximum or median is that a counter could be incremented by several items due to hash collisions. Minimum is chosen to avoid the skew created by high-frequency elements and to be fair to the low-frequency elements.

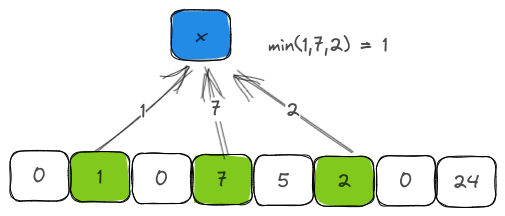
    pub fn estimated_count(&self, item: &T) -> u8 {
        let mut retu = u8::MAX;
        for each in self.get_set_bits(item, self.k, self.m, self.hasher) {
            if self.counter[each] == 0 {
                return 0;
            }
            if self.counter[each] < retu {
                retu = self.counter[each];
            }
        }
        retu
    }

Overflow

Although not included in our implementation, I felt that a discussion on this topic is important.

In our example, we decided that our counter is represented by an unsigned 8-bit integer with a maximum value of 255.  What if subsequent item insertions attempt to increment the value of that counter?  This would result in an overflow and in Rust, a panic. To avoid overflowing, the counter could be capped/saturated at the maximum value. This essentially means that subsequent insertions into that bucket will have no effect on the filter's state for that counter.

There are two common workarounds to solve overflows:

1. Freezing
2. Dynamic resizing

1. Freezing

Freezing is a process where

1. the buckets are scanned for counters that have already reached the maximum value.
2. reset the counter to a threshold value (around 80% of the maximum value). For u8 that's approximately 200.

2. Dynamic resizing

The other simpler yet computationally expensive alternative is to resize the counter to accept larger values. Say, promoting the datatype from u8 to u16.  This involves creating a new counter list, copying the existing counters and replacing the old list with the new one.

Code

Complete code is here.