Quicksorting - 3-way and Dual Pivot
It's no news that Quicksort is considered one of the most important algorithms of the century and that it is the defacto system sort for many languages, including the Arrays.sort in Java.
So, what's new about quicksort?
Well, nothing except that I figured just now (after 2 damn years of release of Java 7) that the Quicksort implementation of the Arrays.sort has been replaced with a variant called Dual-Pivot QuickSort. This thread is not only awesome for this reason but also how humble Jon Bentley and Joshua Bloch really are.
What did I do next?
Just like everybody else, I wanted to implement it and do some benchmarking - against some 10 million integers (random and duplicate).
Oddly enough, I found the following results :
Random Data :
- Quick Sort Basic : 1222 millis
- Quick Sort 3 Way : 1295 millis (seriously !!)
- Quick Sort Dual Pivot : 1066 millis
Duplicate Data :
- Quick Sort Basic : 378 millis
- Quick Sort 3 Way : 15 millis
- Quick Sort Dual Pivot : 6 millis
Stupid Question 1 :
I am afraid that I am missing something in the implementation of 3-way partition. Across several runs against random inputs (of 10 million) numbers, I could see that the single pivot always performs better (although the difference is less than 100 milliseconds for 10 million numbers).
I understand that the whole purpose of making the 3-way Quicksort as the default Quicksort until now is that it does not give 0(n^2) performance on duplicate keys - which is very evident when I run it against duplicate input. But is it true that for the sake of handling duplicate data, a small penalty is taken by 3-way? Or is my implementation bad?
Stupid Question 2
My Dual Pivot implementation (link below) does not handle duplicates well. It takes a sweet forever (0(n^2)) to execute. Is there a good way to avoid this? Referring to the Arrays.sort implementation, I figured out that ascending sequence and duplicates are eliminated well before the actual sorting is done. So, as a dirty fix, if the pivots are equal I fast-forward the lowerIndex until it is different than pivot2. Is this a fair implementation?
else if (pivot1==pivot2){
while (pivot1==pivot2 && lowIndex<highIndex){
lowIndex++;
pivot1=input[lowIndex];
}
}
That's it. That is all I did?
I always find the tracing of the algorithm interesting but with the number of variables in Dual Pivot quicksort, my eyes found it overwhelming while debugging. So, I also went ahead and created trace-enabled implementations (for all 3) so that I could see where the variable pointers currently are.
These trace-enabled classes just overlay where the pointers are below the array values. I hope you find these classes useful.
eg. for a Dual Pivot iteration

Where can you download the code?
The entire project (along with a few lame implementations of DSA) is available on github here. The quicksort classes alone could be found here.
Here's my implementation of the SinglePivot (Hoare), 3-way (Sedgewick) and the new Dual-Pivot (Yaroslavskiy)
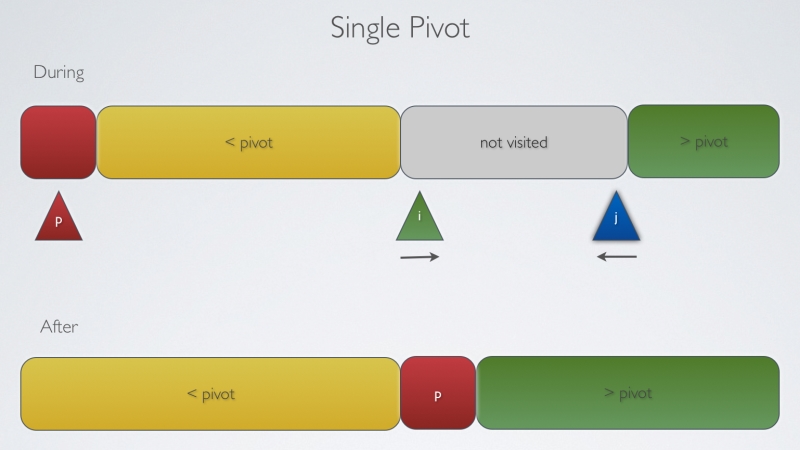
Single Pivot
package basics.sorting.quick;
import static basics.sorting.utils.SortUtils.exchange;
import static basics.sorting.utils.SortUtils.less;
import basics.shuffle.KnuthShuffle;
public class QuickSortBasic {
public void sort (int[] input){
//KnuthShuffle.shuffle(input);
sort (input, 0, input.length-1);
}
private void sort(int[] input, int lowIndex, int highIndex) {
if (highIndex<=lowIndex){
return;
}
int partIndex=partition (input, lowIndex, highIndex);
sort (input, lowIndex, partIndex-1);
sort (input, partIndex+1, highIndex);
}
private int partition(int[] input, int lowIndex, int highIndex) {
int i=lowIndex;
int pivotIndex=lowIndex;
int j=highIndex+1;
while (true){
while (less(input[++i], input[pivotIndex])){
if (i==highIndex) break;
}
while (less (input[pivotIndex], input[--j])){
if (j==lowIndex) break;
}
if (i>=j) break;
exchange(input, i, j);
}
exchange(input, pivotIndex, j);
return j;
}
}
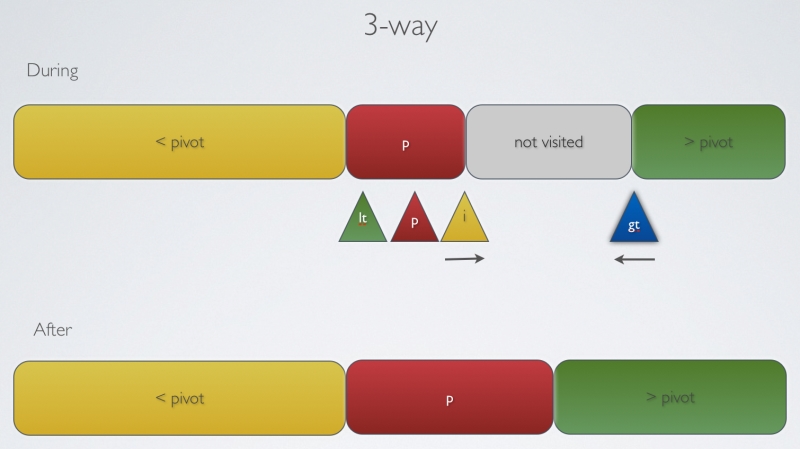
3-way
package basics.sorting.quick;
import static basics.shuffle.KnuthShuffle.shuffle;
import static basics.sorting.utils.SortUtils.exchange;
import static basics.sorting.utils.SortUtils.less;
public class QuickSort3Way {
public void sort (int[] input){
//input=shuffle(input);
sort (input, 0, input.length-1);
}
public void sort(int[] input, int lowIndex, int highIndex) {
if (highIndex<=lowIndex) return;
int lt=lowIndex;
int gt=highIndex;
int i=lowIndex+1;
int pivotIndex=lowIndex;
int pivotValue=input[pivotIndex];
while (i<=gt){
if (less(input[i],pivotValue)){
exchange(input, i++, lt++);
}
else if (less (pivotValue, input[i])){
exchange(input, i, gt--);
}
else{
i++;
}
}
sort (input, lowIndex, lt-1);
sort (input, gt+1, highIndex);
}
}
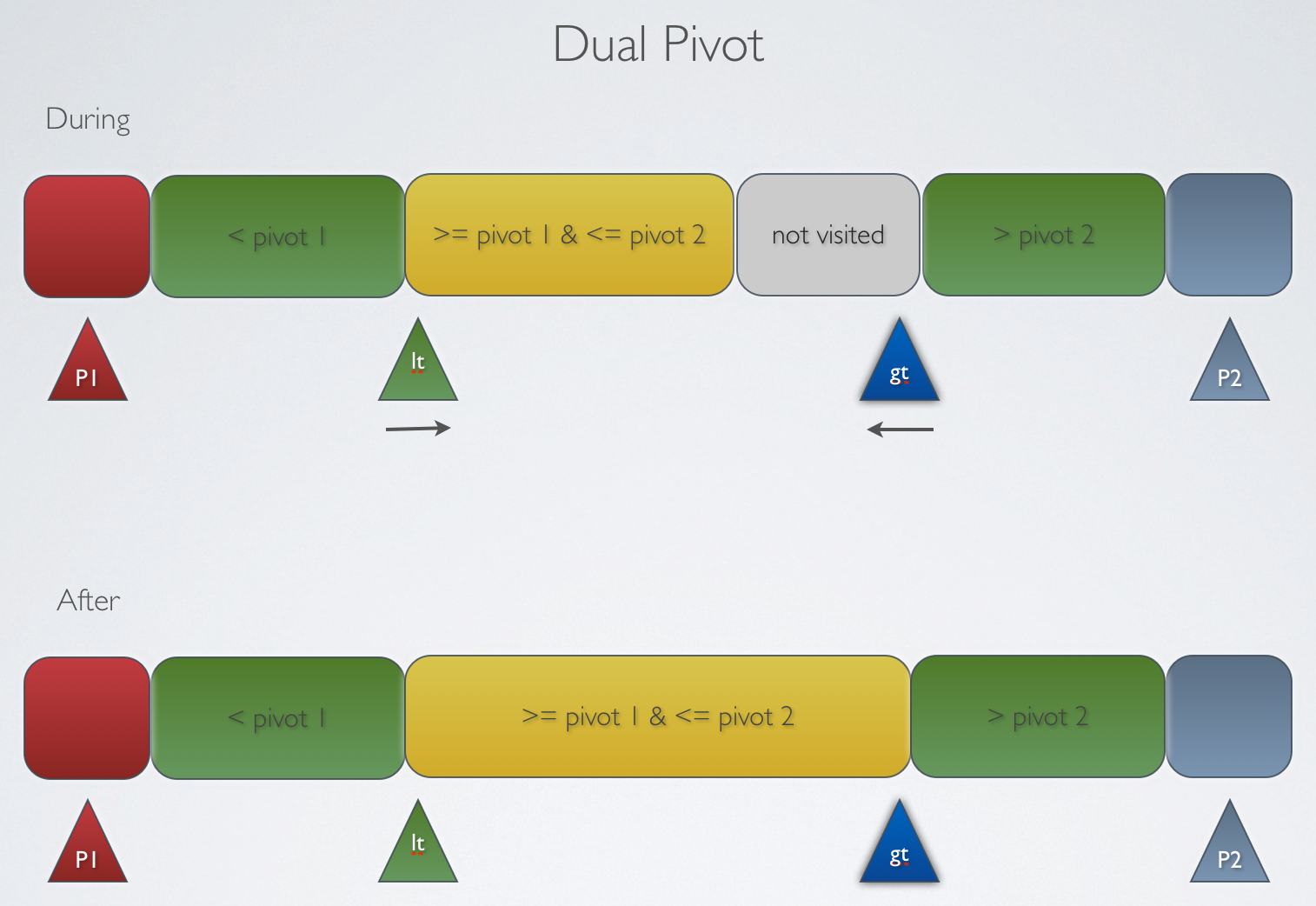
Dual Pivot
package basics.sorting.quick;
import static basics.shuffle.KnuthShuffle.shuffle;
import static basics.sorting.utils.SortUtils.exchange;
import static basics.sorting.utils.SortUtils.less;
public class QuickSortDualPivot {
public void sort (int[] input){
//input=shuffle(input);
sort (input, 0, input.length-1);
}
private void sort(int[] input, int lowIndex, int highIndex) {
if (highIndex<=lowIndex) return;
int pivot1=input[lowIndex];
int pivot2=input[highIndex];
if (pivot1>pivot2){
exchange(input, lowIndex, highIndex);
pivot1=input[lowIndex];
pivot2=input[highIndex];
//sort(input, lowIndex, highIndex);
}
else if (pivot1==pivot2){
while (pivot1==pivot2 && lowIndex<highIndex){
lowIndex++;
pivot1=input[lowIndex];
}
}
int i=lowIndex+1;
int lt=lowIndex+1;
int gt=highIndex-1;
while (i<=gt){
if (less(input[i], pivot1)){
exchange(input, i++, lt++);
}
else if (less(pivot2, input[i])){
exchange(input, i, gt--);
}
else{
i++;
}
}
exchange(input, lowIndex, --lt);
exchange(input, highIndex, ++gt);
sort(input, lowIndex, lt-1);
sort (input, lt+1, gt-1);
sort(input, gt+1, highIndex);
}
}
