Evaluating Infix expression - multiple digits
If you are looking for evaluating an infix expression with parantheses, don't waste your time here. Visit my other fresh write up here


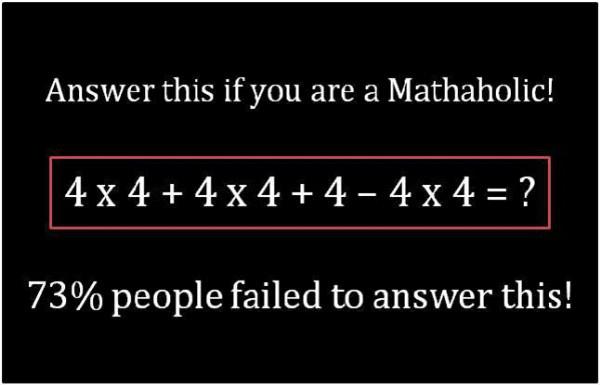
These images have been running around Facebook for a while now. Though it is eye-damaging primary level arithmetic, it is kind of sweet to write it as a program. Just for the fun of it, I created an html page driven by a javascript implementation. Here is the link.
So, essentially the idea is to evaluate the infix notation in a natural way - respecting the operator precedence. (If you consider this as a puzzle, then there are other variations which involves evaluating the expression in such a way that the result is a maximum value/minimum value)
Please note that the algorithm (and therefore, the program), as it stands does not handle parentheses. This is just a two-stack algorithm with a small variation to accommodate numbers more than a digit.
The algorithm goes like this :
1. Initialize two stacks - one for holding values and one for holding operators
2. Read the input expression from left to right - one character at a time.
3. If the character is a space, ignore
4. If the character is a number, then append it to an accumulating variable
(don't push it to the stack yet)
5. If the character is an operator, push the accumulated number to the value stack and
reinitialize the accumulator.
5a. If the current operator is of higher precedence than the first item in the operator stack,
then safely ignore and read further.
5b. If the current operator is of lower precedence than the first item in the operator
stack (peek view), then evaluate the previous set (two from value stack and one
from operator stack) and insert the result into the value stack
5c. Finally, insert the current operator to the operator stack
A Groovy implementation is here :
/**
* Only basic arithmetic operators are supported. However, could easily be
* extended to support any binary operators
*
* This program is not an infix to postfix converter. However, this program does the following
*
* 1) Evaluates a non-parenthesized infix expression and drives it to a final value
* 2) Does not support parentheses
* 3) Supports multiple digits as operands
* 4) Empty space allowed
* 5) Floating point numbers not supported
* 6) Supports only the 4 basic arithmetic operators but could easily be extended to support any other
* binary operation
*
* @author Arun Manivannan
*/
public class InfixToValue {
public static final String OPERATORS="+-/*)" //ignore the "(" as an operator
public static final Map OPERATOR_LEVELS= ["*":1, "/":1, "+":2,"-":2]
public static void main(String[] args) {
String inputExpression="9 - 5+5*0+3" //610
InfixToValue ifixToPfix=new InfixToValue()
ifixToPfix.infixToValue(inputExpression);
}
def infixToValue(String inputExpression) {
Stack<String> expressionStack = new Stack<String>()
Stack<Long> valueStack = new ArrayDeque<Long>() //to hold only non-decimal values
String eachNumber="" //to hold multiple digit values. lame idea, i know, but can't think of anything else at 2 AM
int totalCharInInput=inputExpression.length()
inputExpression.each { eachChar->
totalCharInInput--
println ("each char : "+eachChar)
if (eachChar.trim()==""){
//ignore
}
else if (isValidOperator(eachChar)){
valueStack.push(Long.parseLong(eachNumber)) //push the till now accumulated number to the value stack
eachNumber=""
println ("Iteration Value Stack 1: "+valueStack)
println ("Iteration Expression Stack 1: "+expressionStack)
if (expressionStack.isEmpty()){ //first item
expressionStack.push(eachChar)
}
//if the current operator has higher precedence than the first item in the stack, then it is fine.
//Just insert the incoming
else if (getHigherPrecedenceOperator(eachChar, expressionStack.peek())==eachChar){
expressionStack.push(eachChar)
}
else if (isRightParen(eachChar)){
evaluateAndPushValueToValueStack()
}
//if the current operator is lesser, then the previous higher precedence expression have to be
//evaluated. Else, we would be making wrong calculations while popping off for final evaluation
else{
println ("Value Stack 1: "+valueStack)
println ("Expression Stack 1: "+expressionStack)
//the current operator has higher precedence. Evaluate expression
evaluateAndPushValueToValueStack(valueStack, expressionStack)
//after evaluation of the higher pair, don't forget to insert the current character into the expression stack
expressionStack.push(eachChar)
}
}
else if (eachChar.isNumber()){
eachNumber+=eachChar
if (totalCharInInput==0){
valueStack.push(Long.parseLong(eachNumber)) //the last element
}
}
/*else {
//other input (alphabets and special chars) are treated as garbage
}*/
}
println ("Expression stack " +expressionStack);
println ("Value stack : "+valueStack)
while (!expressionStack.empty){
evaluateAndPushValueToValueStack(valueStack,expressionStack)
}
println ("Final value : "+valueStack)
}
boolean isRightParen(String operator) {
operator==")"?true:false
}
boolean isLeftParen(String operator) {
operator=="("?true:false
}
private void evaluateAndPushValueToValueStack(Stack<Long> valueStack, Stack<String> expressionStack) {
Long firstOperand=valueStack.pop()
Long secondOperand=valueStack.pop()
println ("Value stack : "+firstOperand+ ":"+ secondOperand )
Long evaluatedValue = this.evaluate(secondOperand, firstOperand, expressionStack.pop()) //intermediate result
valueStack.push(evaluatedValue)
}
Long evaluate(Long firstOperand, Long secondOperand, String operator) {
Long returnValue
switch (operator) {
case "+" :
returnValue=firstOperand+secondOperand
break
case "-" :
returnValue=firstOperand-secondOperand
break;
case "*":
returnValue=firstOperand*secondOperand
break
case "/":
if (secondOperand==0){ //cheating death by zero
returnValue=0
}
else{
returnValue=firstOperand/secondOperand
}
break;
}
}
boolean isValidOperator(String input) {
OPERATORS.contains(input)?true:false
}
String getHigherPrecedenceOperator(String firstOperator, String secondOperator){
OPERATOR_LEVELS[firstOperator]<OPERATOR_LEVELS[secondOperator]?firstOperator:secondOperator
}
}
