Find Continuous subarray with maximum sum problem - Kadane's algorithm

Update : Previous version of the code failed for some inputs, as pointed out by @Thinker in the first comment. Changes to the program and the presentation were made. Tested to satisfy most conditions that I could google for.

In a desperate attempt to increase my sad looking stackoverflow reputation, I replied to an old but interesting problem.

The problem goes like this :

Given Random integers in array. Find the greatest sum of a continuous subset

The problem is otherwise known as the Maximum subarray problem and is beaten to death numerous times.

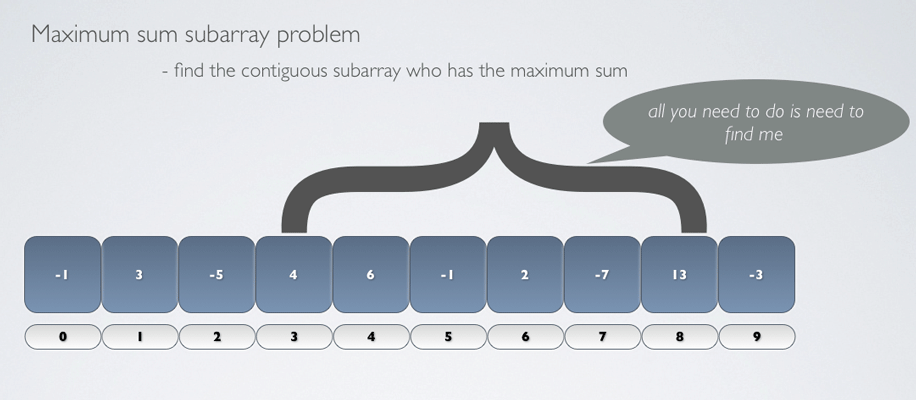
So, instead of just translating a Python program into Java, I decided to pull together some slides which explains how this algorithm works.

And to bore you to death, here is the Java version of the modified algorithm :

package me.rerun;

public class Kadane {

    public static void main(String[] args) {
    	int[] intArr={3, -1, -1, -1, -1, -1, 2, 0, 0, 0 };
    	//int[] intArr = {-1, 3, -5, 4, 6, -1, 2, -7, 13, -3};
    	//int[] intArr={-6,-2,-3,-4,-1,-5,-5};
        findMaxSubArray(intArr);
    }

    public static void findMaxSubArray(int[] inputArray){

        int maxStartIndex=0;
        int maxEndIndex=0;
        int maxSum = Integer.MIN_VALUE; 

        int cumulativeSum= 0;
        int maxStartIndexUntilNow=0;
        		
        for (int currentIndex = 0; currentIndex < inputArray.length; currentIndex++) {
        	
            int eachArrayItem = inputArray[currentIndex];
            
            cumulativeSum+=eachArrayItem;

            if(cumulativeSum>maxSum){
                maxSum = cumulativeSum;
                maxStartIndex=maxStartIndexUntilNow;
                maxEndIndex = currentIndex;
            }
            else if (cumulativeSum<0){
            	maxStartIndexUntilNow=currentIndex+1;
            	cumulativeSum=0;
            }
        }

        System.out.println("Max sum         : "+maxSum);
        System.out.println("Max start index : "+maxStartIndex);
        System.out.println("Max end index   : "+maxEndIndex);
    }
   
}

Rajesh was kind enough to write the implementation in Scala. Sweet huh?